ML Lecture: Word Embedding
介紹關於NLP中詞嵌入(word embedding)處理手法,基於降維思想提供count-based, prediction-based兩種方法。主要應用在機器問答、機器翻譯、圖像分類、文檔嵌入等方面。
Introduction
詞嵌入(word embedding)是降維算法(Dimension Reduction)的典型應用
那如何用vector來表示一個word呢?
-
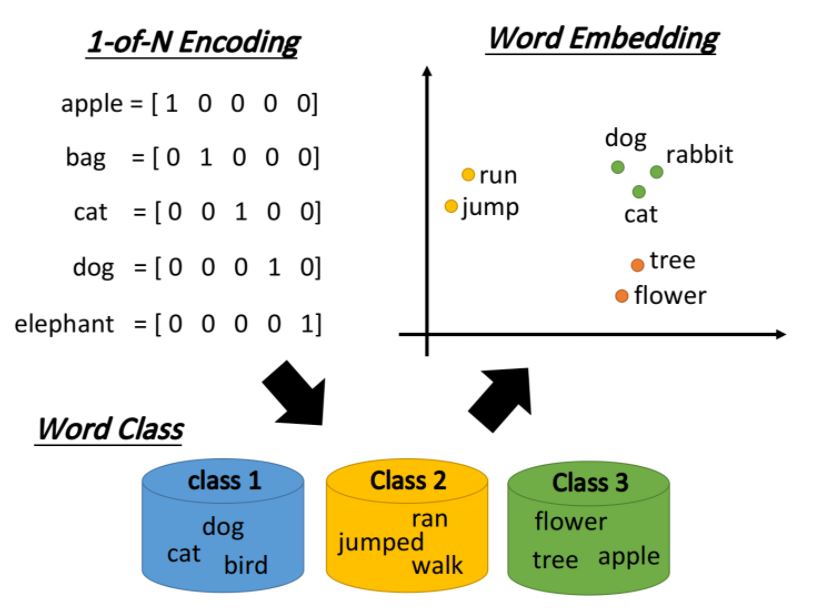
1-of-N Encoding 將所有的單詞用one-hot encoding方式轉成向量,而向量的長度即世界上所有單詞的數量。例如: I → [1,0,0,0,…,0]; apple → [0,1,0,0,…,0]。 但是,任意兩個向量的差異(相似性,距離)皆一樣,導致同類單詞無相關性。
-
Word Class 把具相同性質的單詞進行分群(clustering),得到多個class以代表該單詞。 但是,不同class的關聯依然無法被良好表達出來。
-
Word Embedding 詞嵌入(Word Embedding)把每一個word都投影到高維空間上,當然這個空間的維度要遠比1-of-N Encoding的維度低,假如後者有10萬維,那前者只需要50 ~ 100維就夠了,這實際上也是Dimension Reduction的過程
類似語義(semantic)的詞彙,在這個word embedding的投影空間上是比較接近的,而且該空間裡的每一維都可能有特殊的含義
假設詞嵌入的投影空間如下圖所示,則橫軸代表了生物與其它東西之間的區別,而縱軸則代表了會動的東西與靜止的東西之間的差別
Word Embedding
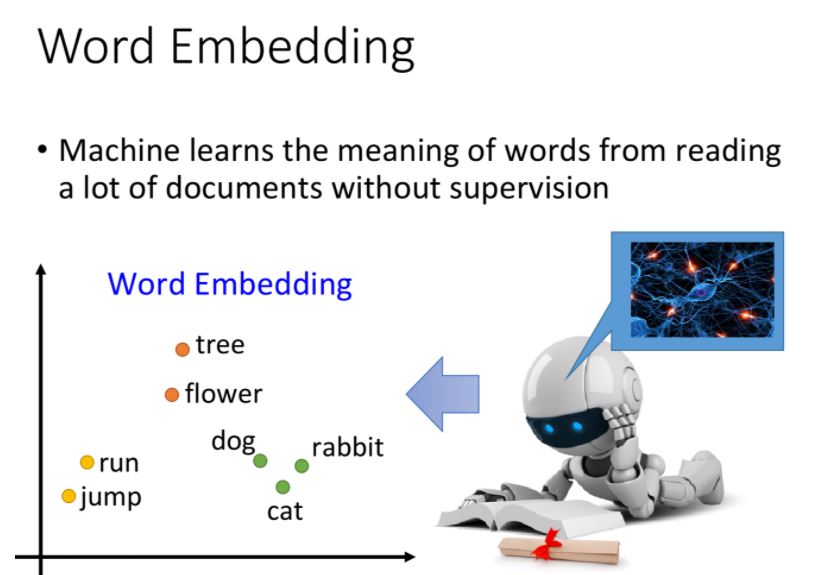
word embedding是一個無監督的方法(unsupervised approach),只要讓機器閱讀大量的文章,它就可以知道每一個詞彙embedding之後的向量應該長什麼樣子。
我們的任務就是訓練一個neural network,input是詞彙,output則是它所對應的word embedding vector,實際訓練的時候我們只有data的input,該如何解這類問題呢?
之前提到過一種基於神經網絡的降維方法,Auto-Encoder,就是訓練一個model,讓它的輸入等於輸出,取出中間的某個隱藏層就是降維的結果,自編碼(Auto-Encoder)的本質就是通過自我壓縮和解壓的過程來尋找各個維度之間的相關信息;但word embedding這個問題是不能用Auto-encoder來解的,因為輸入的向量通常是1-of-N編碼,各維無關,很難通過自編碼的過程提取出什麼有用信息。
那怎麼辦呢? Basic Idea: 每一個詞彙的含義都可以根據它的上下文來得到
比如機器在不同地方閱讀到了“馬英九520宣誓就職”、“蔡英文520宣誓就職”,就會發現“馬英九”和“蔡英文”前後都有類似的文字內容,於是機器就可以推測“馬英九”和“蔡英文”這兩個詞彙代表了可能有同樣地位的東西,即使它並不知道這兩個詞彙是人名。
怎麼用這個思想來找出word embedding後的vector呢?有兩種做法:
- Count based
- Prediction based
Count based
假設\(w_i\)和\(w_j\)這兩個詞彙常常在同一篇文章中出現(co-occur),其中word vector分別用\(V(w_i)\)和\(V(w_j)\)來表示,則\(V(w_i)\)和\(V(w_j)\)會比較相似、接近。
如何找到\(V(w_i)\)和\(V(w_j)\) ?
假設\(N_{i,j}\)是\(w_i\)和\(w_j\)在相同文章裡同時出現的次數,我們希望它與的內積越接近越好(i.e. \(\min{N_{i,j} - V(w_i)V(w_j) }\),這個思想和之前的文章中提到的矩陣分解(matrix factorization)的思想其實是一樣的
這種方法有一個很代表性的例子是Glove Vector, research by stanford.
Prediction based
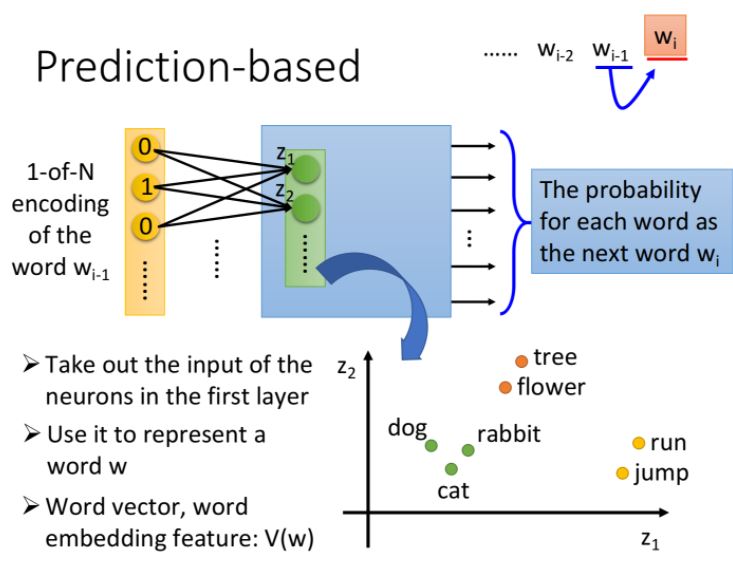
概念為給定一個句子,希望模型能夠根據當前的word \(w_{i-1}\),預測下一個出現的\(w_i\)是什麼。
首先用1-of-N encoding把\(w_{i-1}\)作為neural network的input,而output則為與\(w_i\)相同長度的機率向量,目標為預測\(w_i\)。
把第一個hidden layer的input \(z_1,z_2,...\)拿出來,它們所組成的\(Z\)就是word的另一種表示方式,當我們input不同的詞彙,向量就會發生變化。
也就是說,第一層hidden layer的維數可以由我們決定,而它的input又唯一確定了一個word,因此提取出第一層hidden layer的input,實際上就得到了一組可以自定義維數的Word Embedding的向量。
Whay prediction works
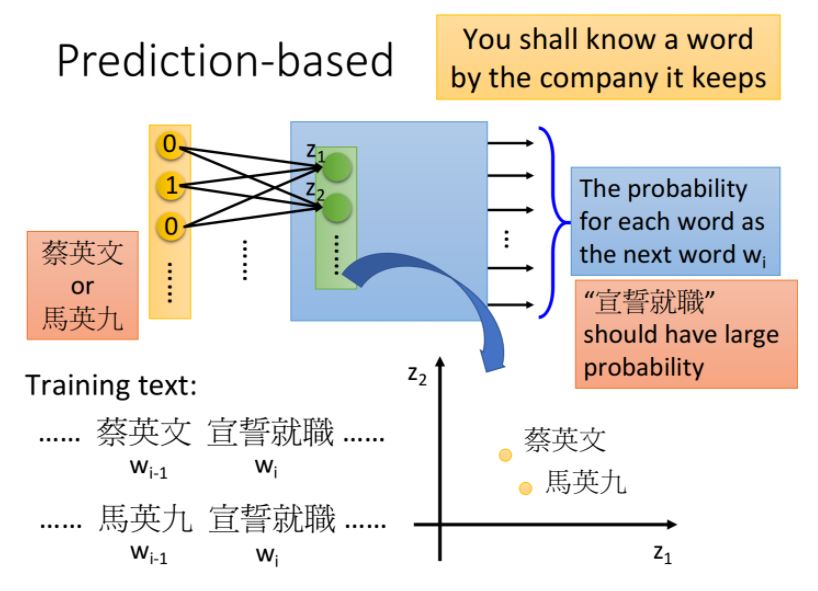
prediction-based方法根據詞彙的上下文來了解該詞彙的含義。
假設在兩篇文章中,“蔡英文”和“馬英九”代表 \(w_{i-1}\),“宣誓就職”代表\(w_i\),希望輸入“蔡英文”或“馬英九”,輸出的vector中對應“宣誓就職”詞彙的概率值是高的。
為了使這兩個不同的input通過NN能得到相同的output,就必須在進入hidden layer之前,就通過weight的轉換將這兩個input vector投影到位置相近的低維空間上
也就是說,儘管兩個input vector作為1-of-N編碼看起來完全不同,但經過參數的轉換,將兩者都降維到某一個空間中,在這個空間裡,經過轉換後的new vector 1和vector 2是非常接近的,因此它們同時進入一系列的hidden layer,最終輸出時得到的output是相同的
因此,詞彙上下文的聯繫就自動被考慮在這個prediction model裡面
總結一下,對1-of-N編碼進行Word Embedding降維的結果就是神經網絡模型第一層hidden layer的輸入向量\([z_1, z_2, ...]^T\),該向量同時也考慮了上下文詞彙的關聯,我們可以通過控制第一層hidden layer的大小從而控制目標降維空間的維數
Sharing Parameters
你可能會覺得通過當前詞彙預測下一個詞彙這個約束太弱了,由於不同詞彙的搭配千千萬萬,即便是人也無法準確地給出下一個詞彙具體是什麼
你可以擴展這個問題,使用10個及以上的詞彙去預測下一個詞彙,可以幫助得到較好的結果
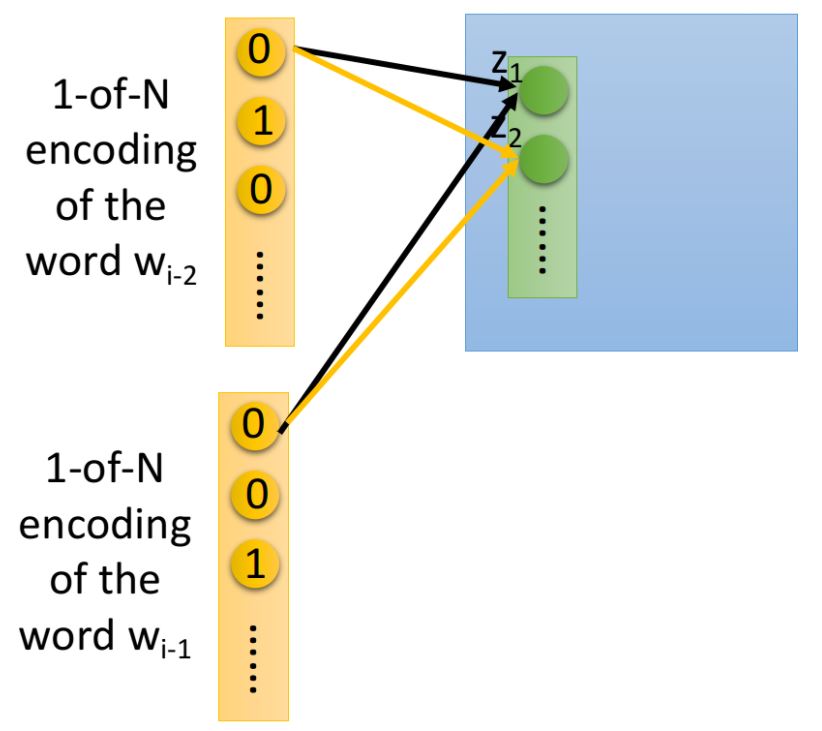
這裡用2個詞彙舉例,如果是一般是神經網絡,我們直接把和這兩個vector拼接成一個更長的vector作為input即可
但實際上,我們希望和相連的weight與和相連的weight是tight在一起的,簡單來說就是與的相同dimension對應到第一層hidden layer相同neuron之間的連線擁有相同的weight,在下圖中,用同樣的顏色標註相同的weight:
如果我們不這麼做,那把同一個word放在的\(w_{i-2}\)和\(w_{i-1}\)的位置,得到的Embedding結果是會不一樣的,把兩組weight設置成相同,可以使與的相對位置不會對結果產生影響
除此之外,這麼做還可以通過共享參數的方式有效地減少參數量,不會由於input的word數量增加而導致參數量劇增
Formulation
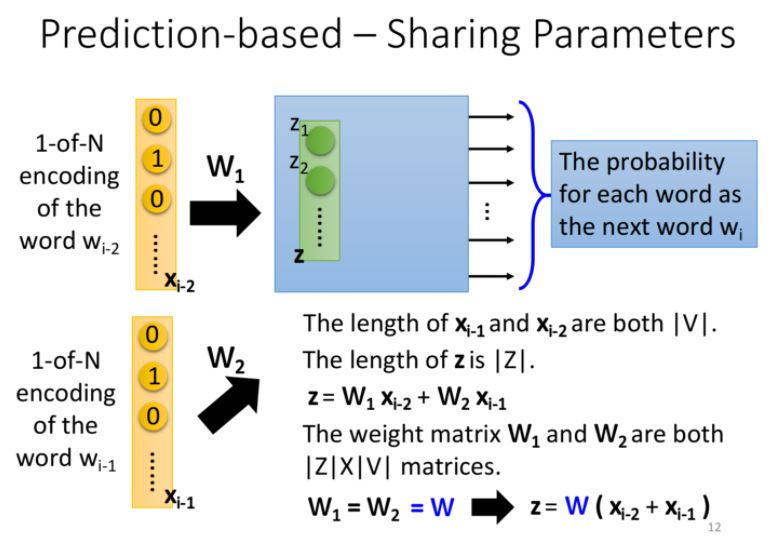
| 假設\(w_{i-2}\)的1-of-N為\(x_{i-2}\),\(w_{i-1}\)為\(x_{i-1}\),維數均為$$ | V | $$,表示數據中的words總數 |
| hidden layer的input為向量\(z\),長度為$$ | Z | $$,表示降維後的維數 |
| 其中\(W_1\)和\(W_2\)都是$$ | Z | \times | V | $$的weight matrix |
我們強迫讓\(W_1 = W_2 = W\),此時\(z = W(x_{i-2}+x_{i-1})\) 因此,只要我們得到了這組參數\(W\),就可以與1-of-N編碼相乘得到word embedding的結果
In Practice
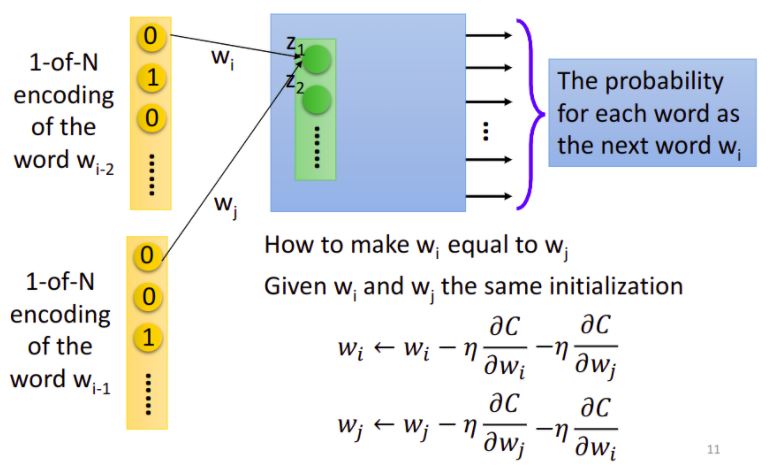
那在實際操作上,我們如何保證\(W_1\)和\(W_2\)一樣呢?
- 首先在訓練的時候就要給一樣的初始值
- \(w_i\)和\(w_j\)的更新過程相同
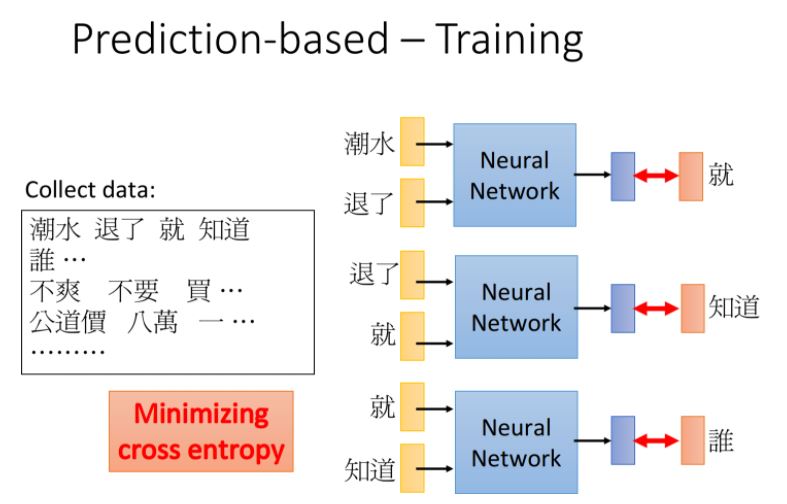
如何去訓練這個神經網絡呢?注意到這個NN完全是unsupervised,你只需要上網爬一下文章數據直接餵給它即可
比如餵給NN的input是“潮水”和“退了”,希望它的output是“就”,之前提到這個NN的輸出是一個由概率組成的vector,而目標“就”是只有某一維為1的1-of-N編碼,我們希望minimize它們之間的cross entropy,也就是使得輸出的那個vector在“就”所對應的那一維上概率最高
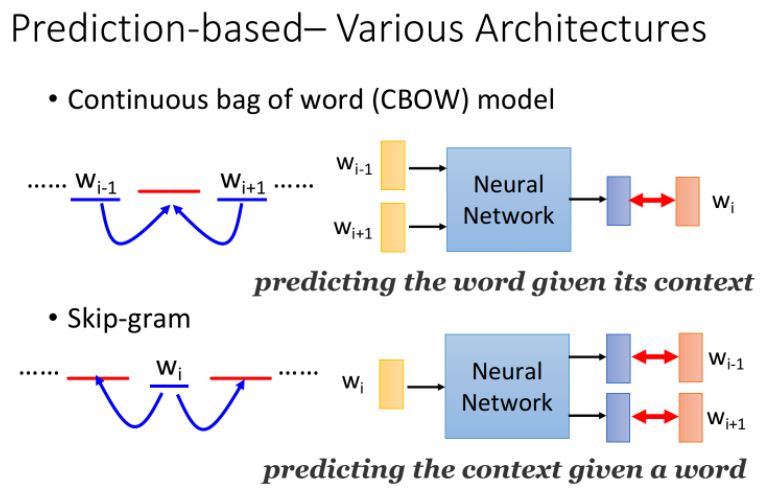
Various Architectures
除了上面的前面預測後面,Prediction-based方法還可以有多種變形:
-
CBOW(Continuous bag of word model)
拿前後的詞彙去預測中間的詞彙
-
Skip-gram
拿中間的詞彙去預測前後的詞彙