ML Lecture: Recurrent Neural Network

Introduction

Analysis the meaning of a phrase.

Slot Filling

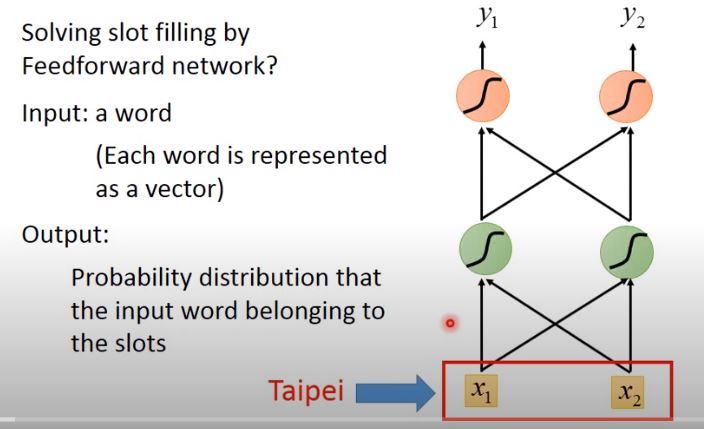
Input a word vector to the Network. Output the probability of that input word belong to the slots.

  • Slot: the meaning of a phrase that is of interest. (e.g. Destination, time of arrival)

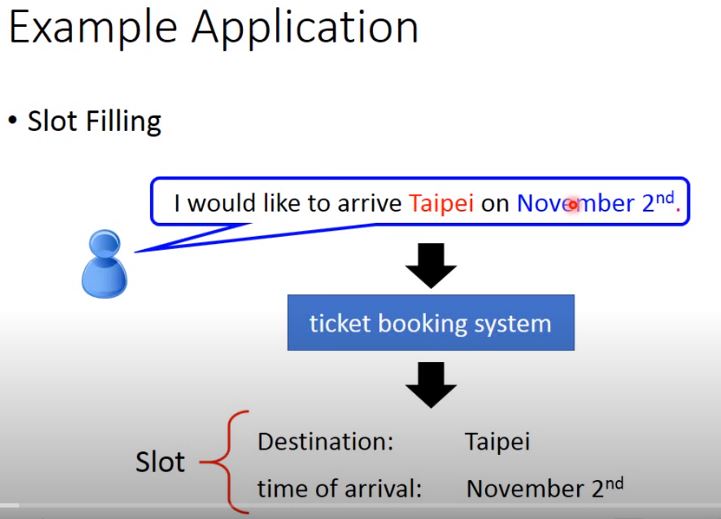
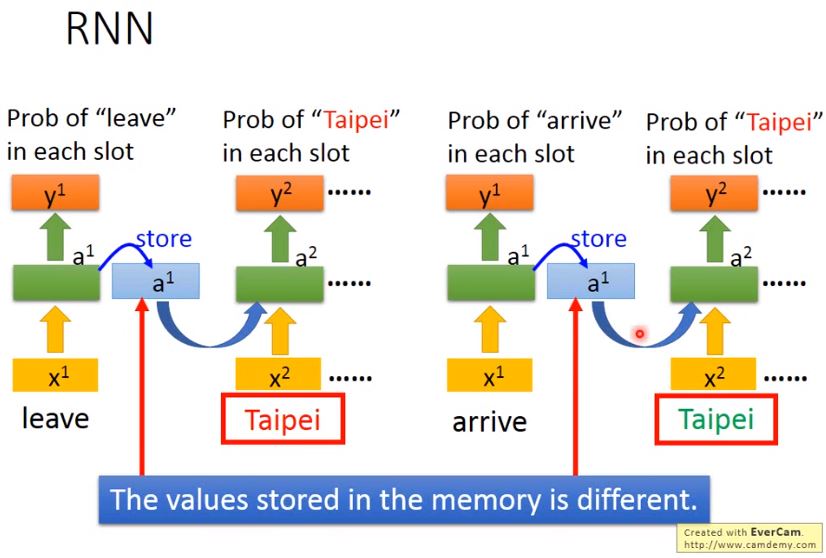
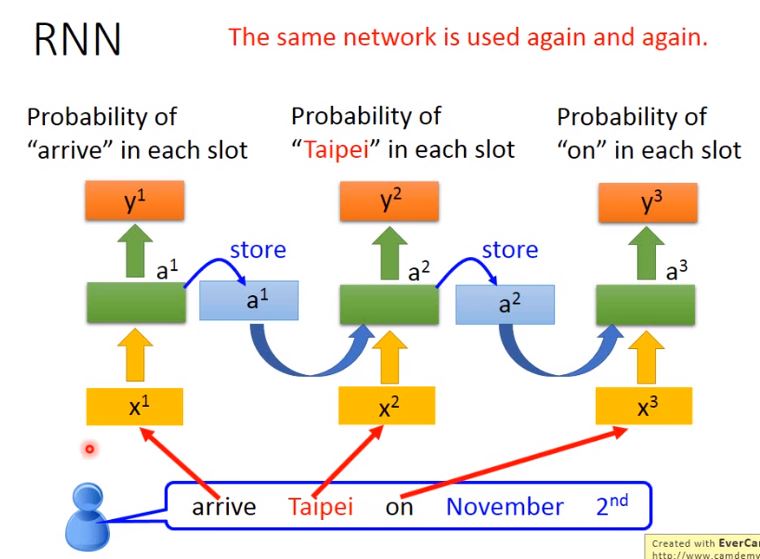
但這樣做會有一個問題，該神經網絡會先處理“arrive”和“leave”這兩個詞彙，然後再處理“Taipei”，這時對NN來說，輸入是相同的，它沒有辦法區分出“Taipei”是出發地還是目的地。

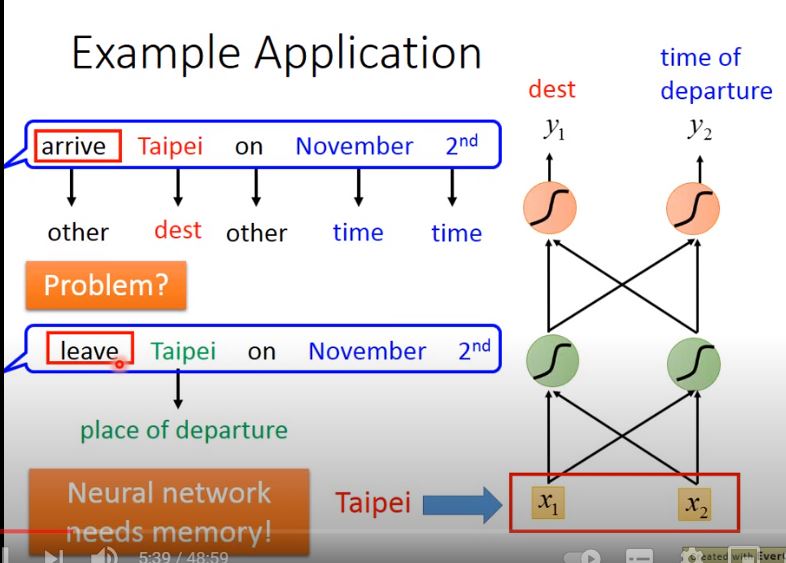
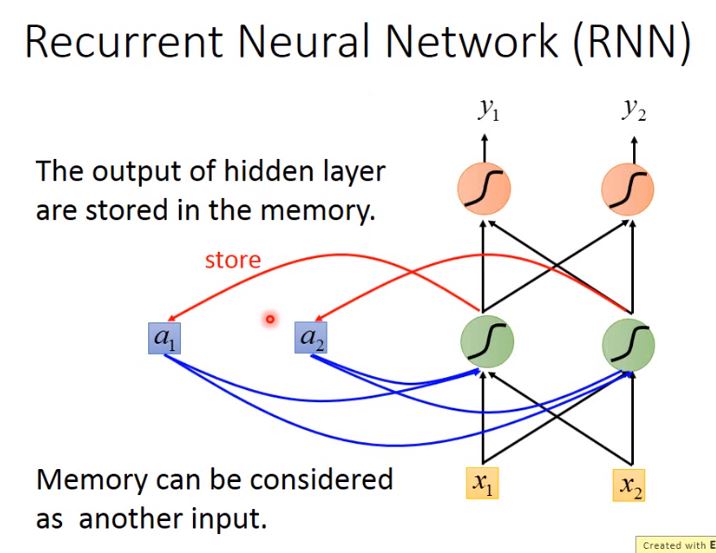
這個時候我們就希望神經網絡是有記憶的，如果NN在看到“Taipei”的時候，還能記住之前已經看過的“arrive”或是“leave”，就可以根據上下文得到正確的答案。 這種有記憶力的神經網絡，就叫做Recurrent Neural Network(RNN)。

在RNN中，hidden layer每次產生的output \(a_1\)、\(a_2\)，都會被存到memory裡，下一次有input的時候，這些neuron就不僅會考慮新輸入的\(x_1\)、\(x_2\)，還會考慮存放在memory中的\(a_1\)、\(a_2\)

Note：

  1. 在input之前，要先給內存裡的\(a_1\)、\(a_2\)賦初始值，比如0
  2. 改變輸入序列的順序會導致最終輸出結果的改變(Changing the sequence order will change the output)

Slot Filling with RNN

用RNN處理Slot Filling的流程舉例如下：

  • “arrive”的vector作為\(x_1\)輸入RNN，通過hidden layer生成\(a_1\)，再根據\(a_1\)生成\(y_1\)，表示“arrive”屬於每個slot的概率，其中\(a_1\)會被存儲到memory中
  • “Taipei”的vector作為\(x_2\)輸入RNN，此時hidden layer考慮\(x_2\)和存放在memory中的\(a_1\)，生成\(a_2\)，再根據\(a_2\)生成\(y_2\)，表示“Taipei”屬於某個slot的概率，此時再把\(a_2\)存到memory中
  • 依次類推，直到所有word vector跑完Network

這個時候，即使輸入同樣是“Taipei”，我們依舊可以根據前文的“leave”或“arrive”得到不一樣的輸出(e.g. 分別屬於Destination與Source的機率)

Elman Network & Jordan Network

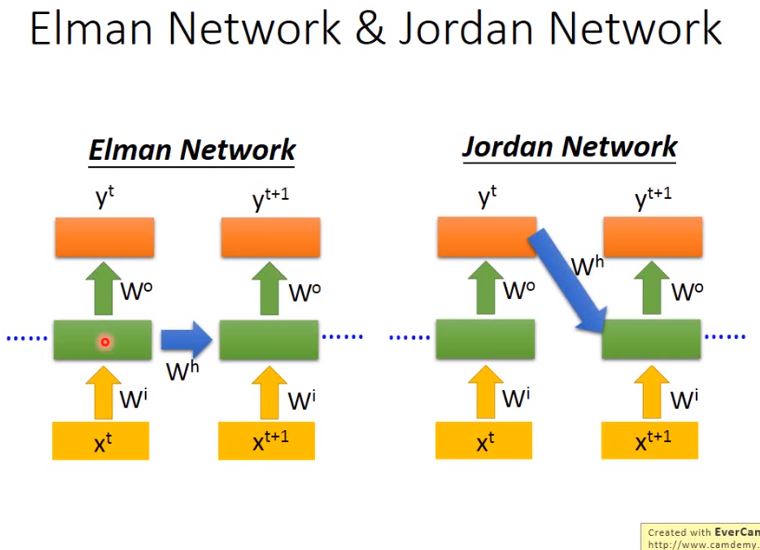
  • Elman: store output of Hidden layer into memory.
  • Jordan: store output of Output layer into memory.

經驗上，由於hidden layer沒有明確的訓練目標(w)，而整個NN具有明確的目標(y)，因此Jordan Network的表現會更好一些

Bidirectional RNN

RNN 可以是雙向的，同時訓練一對正向和反向的RNN，把它們對應的hidden layer \(x^t\)拿出來，都接給一個output layer，得到最後的\(y^t\)

好處: NN它能夠看到資料範圍是比較廣的，RNN在產生的\(y^{t+1}\)時候，

  1. 從句首\(x^1\)開始到\(x^{t+1}\)的輸入
  2. 從句尾\(x^n\)一直到\(x^{t+1}\)的輸入

這就相當於RNN在看了整個句子之後，才決定每個詞彙具體要被分配到哪一個槽中，這會比只看句子的前一半要更好。

LSTM (Long Short-term Memory)

  • Gate is designed to control whether a comming value pass through. Three gates:
    • input: 當某個neuron的輸出想要被寫進memory cell，它就必須要先經過一道叫做input gate的閘門，如果input gate關閉，則任何內容都無法被寫入，而關閉與否、什麼時候關閉，都是由神經網絡自己學習到的
    • forget: 決定了什麼時候需要把memory cell裡存放的內容忘記清空，什麼時候依舊保存
    • output: 決定了外界是否可以從memory cell中讀取值，當output gate關閉的時候，memory裡面的內容同樣無法被讀取

整個LSTM可以看做是4個input，1個output：

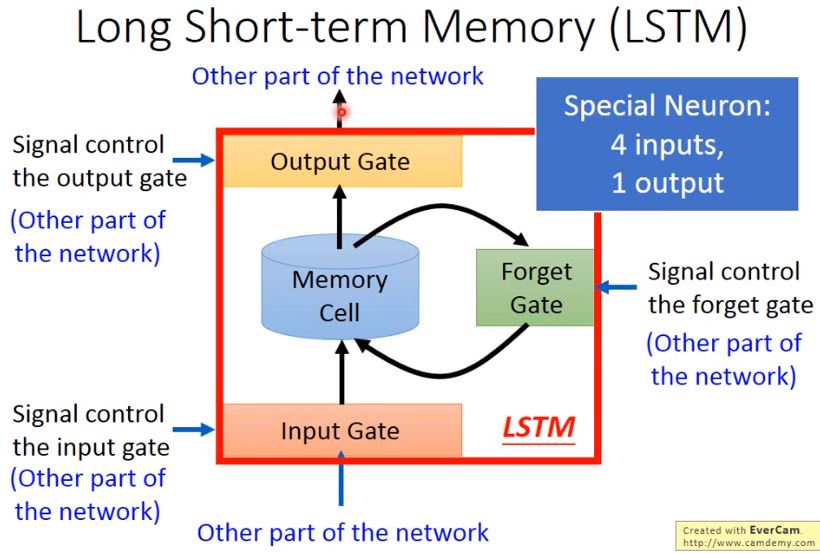
  • 4個input=想要被存到memory cell裡的值+操控input gate的信號+操控output gate的信號+操控forget gate的信號
  • 1個output=想要從memory cell中被讀取的值

冷知識：可以被理解為比較長的短期記憶，因此是short-term，而非是long-short term

Memory Cell

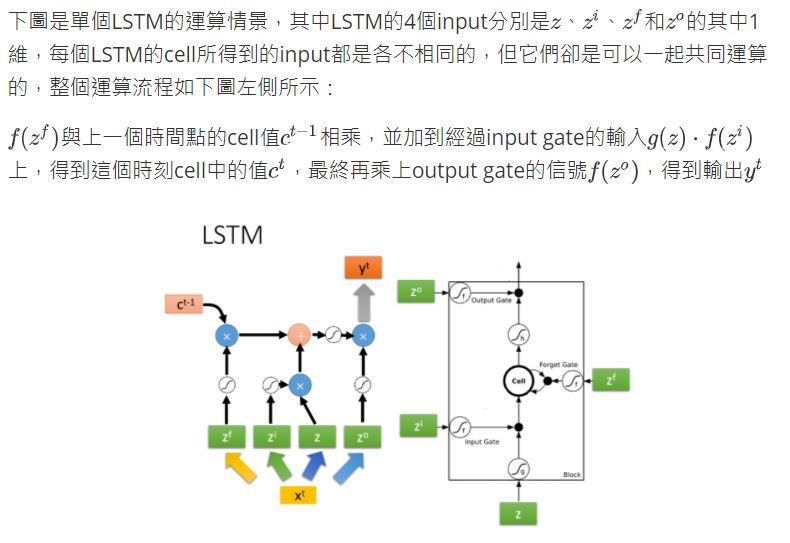
如果從表達式的角度看LSTM，它比較像下圖中的樣子

  • \(z\)是想要被存到cell裡的輸入值
  • \(z_i\)是操控input gate的信號
  • \(z_o\)是操控output gate的信號
  • \(z_f\)是操控forget gate的信號
  • \(a\)是綜合上述4個input得到的output值

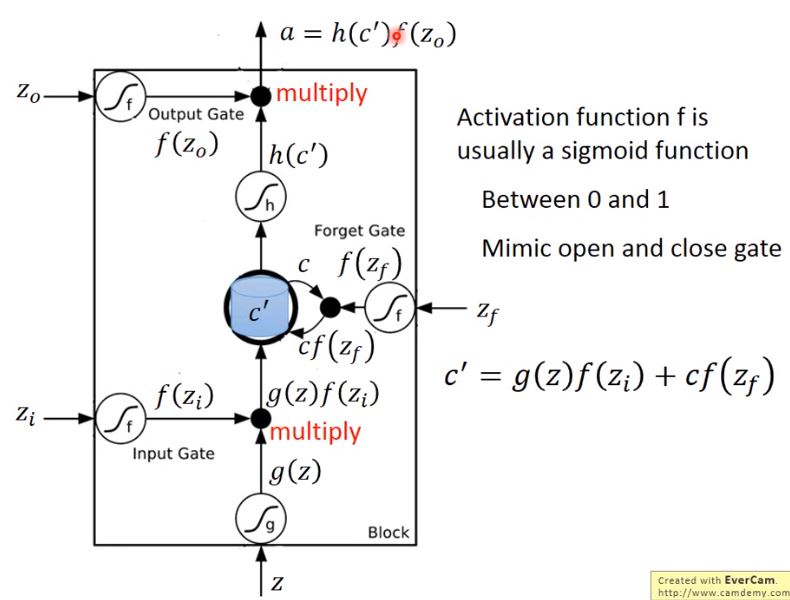
把\(z\)、\(z_i\)、\(z_o\)、\(z_f\)通過activation function，分別得到\(g(z)\)、\(f(z_i)\)、\(f(z_o)\)、\(f(z_f)\)

其中對\(z_i\)、\(z_o\)、\(z_f\)來說，它們通過的激活函數一般會選sigmoid function，因為它的輸出在0 ~ 1之間，代表gate被打開的程度。

令\(g(z)\)與\(f(z_i)\)相乘得到\(g(z)f(z_i)\)，然後把原先存放在cell中的\(c\)與\(f(z_f)\)相乘得到\(c f(z_f)\)，兩者相加得到存在memory中的新值\(c' = g(z)f(z_i) + c f(z_f)\)

  • 若\(f(z_i) = 0\)，則相當於沒有輸入，若\(f(z_i) = 1\)，則相當於直接輸入\(g(z)\)
  • 若\(f(z_f) = 1\)，則保存舊的值\(c\)並加到新的值上，若\(f(z_f) = 0\)，則舊的值將被遺忘清除

從中也可以看出，forget gate的邏輯與我們的直覺是相反的，控制信號打開表示記得，關閉表示遺忘

此後，\(c'\)通過激活函數得到\(h(c')\)，與output gate的\(f(z_o)\)相乘，得到輸出\(a = h(c')f(z_o)\)

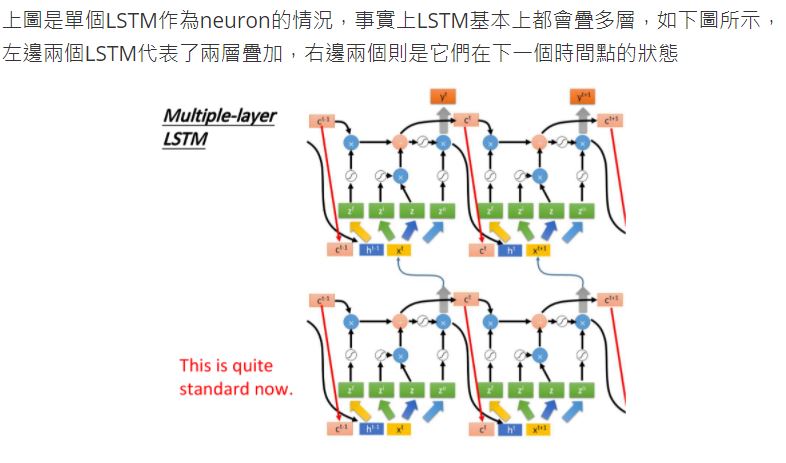
LSTM Structure and Neuron

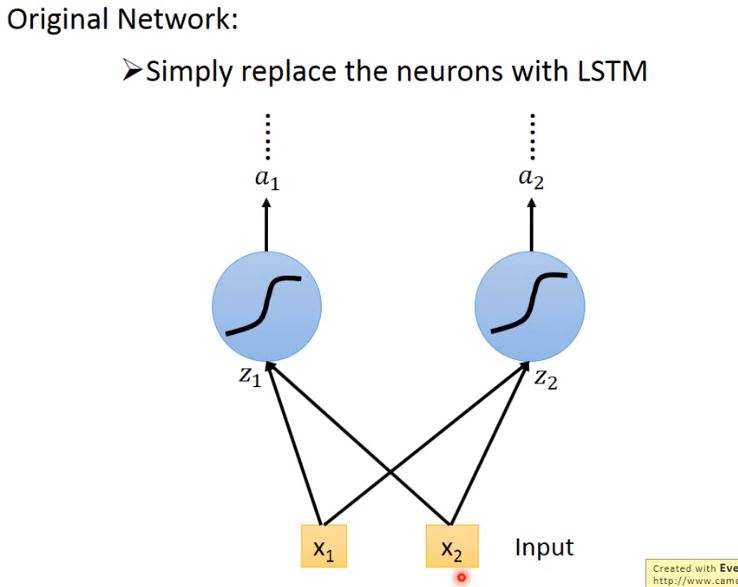
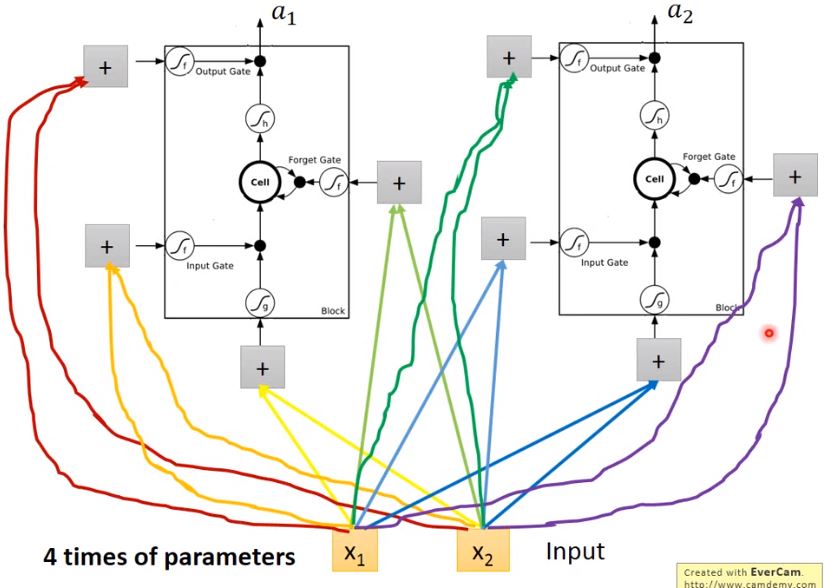
你可能會覺得上面的結構與平常所見的神經網絡不太一樣，實際上我們只需要把LSTM整體看做是下面的一個neuron即可 假設目前我們的hidden layer只有兩個neuron，則結構如下圖所示：

  • 輸入\(x_1\)、\(x_2\)會分別乘上四組不同的weight，作為neuron的輸入以及三個狀態門的控制信號
  • 在原來的neuron裡，1個input對應1個output，而在LSTM裡，4個input才產生1個output，並且所有的input都是不相同的
  • 從中也可以看出LSTM所需要的參數量是一般NN的4倍

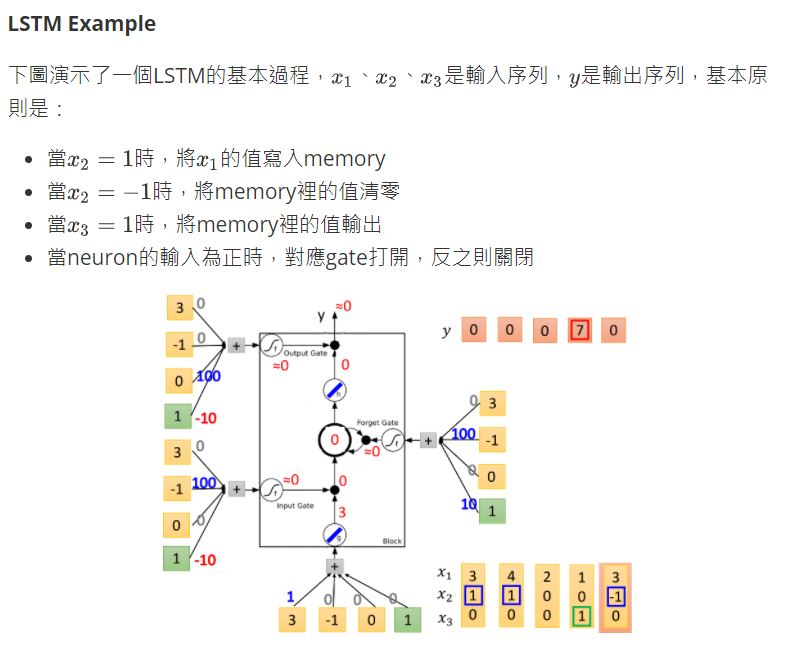
LSTM for RNN

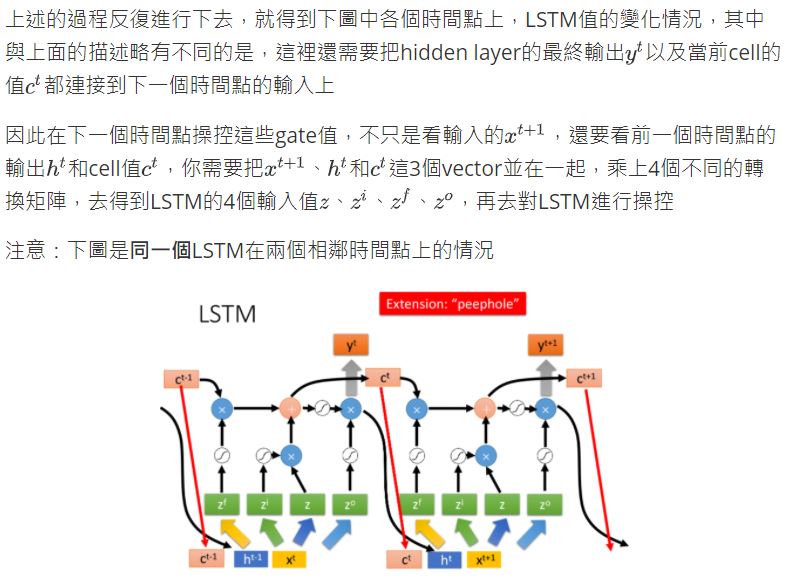
從上圖中你可能看不出LSTM與RNN有什麼關係，接下來我們用另外的圖來表示它

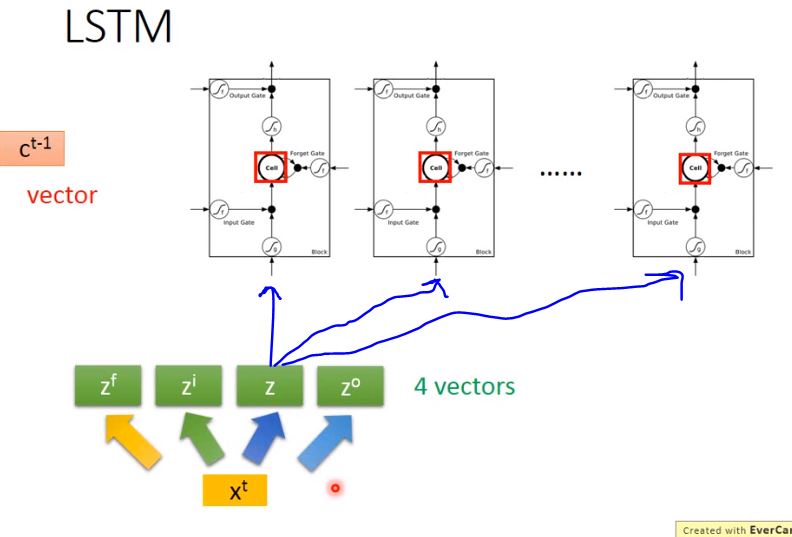
假設我們現在有一整排的LSTM作為neuron，每個LSTM的cell裡都存了一個scalar值，把所有的scalar連接起來就組成了一個vector, \(c^{t-1}\).

在時間點\(t\)，輸入了一個vector \(x^t\)，它會乘上一個matrix，通過轉換得到vector \(z\)，而\(z\)的每個dimension就代表了操控每個LSTM的輸入值，同理經過不同的轉換得到\(z^i\)、\(z^f\)和\(z^o\)，得到操控每個LSTM gate信號

← previous page